面積について、小学校で習う知識で考えてみました。面積を求める公式は色々ありますが、小学校で習う範囲では、長方形の面積の公式を知っておけば何とかなると思います。
それでは、見ていきましょう。
面積の求め方
長方形
長方形とは、四つの角がすべて直角であるような四角形のことです。長方形の中で、四辺の長さが同じ図形を正方形といいます。
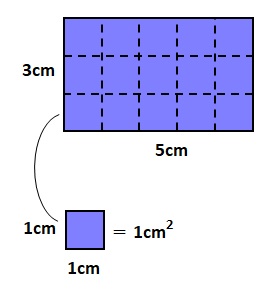
四辺の長さが1の正方形の面積を1として、この正方形が何個敷き詰められるかを考えて、長方形の面積を計算します。なお、面積の単位は長さの2乗です。面積の単位がcm2 ならば、日本語では「平方センチメートル」と読みます。
例えば、縦の長さが3cmで横の長さが5cmの長方形の面積を求めたいとします。この長方形には、面積1cm2の正方形が縦方向に(3÷1)個、横方向に(5÷1)個並べられるので、正方形の個数を求めればよいことになります。計算式は3×5となりますので、面積は15cm2になります。これより、長方形の面積を求める公式は、縦×横となることが分かります。
長方形の面積を求める公式は縦×横だと習ったカズくん、ナナさん、ハジメくんとユイさんの4人が班になって、長方形の面積を求めることになりました。ナナさんとハジメくんは4×2=8と計算しました。一方、カズくんとユイさんは2×4=8と計算しました。答えは8cm2で同じですが、どちらが正しい式で計算しているでしょうか。
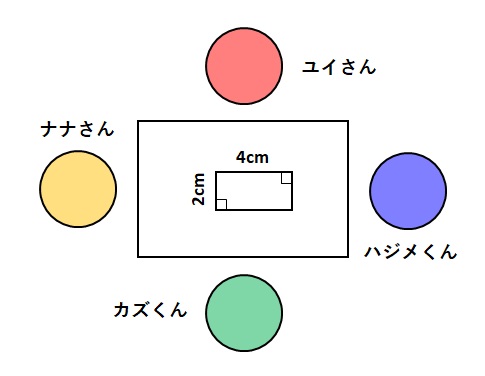
どちらも正しいですね。これは、長方形の縦と横をどちらにとるかの視点の違いによるものですね。つまり、長方形の面積を求める公式は、縦×横、横×縦のどちらでも良いということになりますね。このように掛け算の順序を入れ替えても等式が成り立つ(縦×横=横×縦)とき、交換法則が成り立つといいます。なお、この交換法則が成り立たないこともありますので、間違っても「掛け算なら交換法則が成り立つ」と暗記しないでください。行列の積などは交換法則が成り立ちませんから。
平行四辺形
平行四辺形とは、二組の対辺がともに平行である四角形のことです。
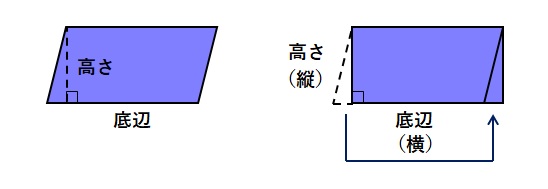
1つの頂点から底辺に向けて垂線を引き、三角形部分を切り取ってみます。切り取った三角形を反対側に移動させると長方形になります。長方形の面積は縦×横で求まりますので、平行四辺形の面積も求められます。ただし、平行四辺形は底辺と高さで表記します。つまり、平行四辺形の面積を求める公式は、底辺×高さになります。なお、高さとは垂直方向の長さのことをいいます。長方形では縦と横が直角なので、どちらかが高さといえます。
台形
台形とは、一組の対辺が平行である四角形のことです。
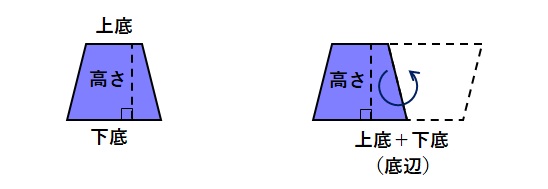
平行でない辺の中点を回転軸として回転させて、元の台形と合わせると平行四辺形になります。平行四辺形の面積は、底辺×高さで求まりますので、その面積の半分が台形の面積となります。台形では平行部の辺の長さが異なりますので、片方の辺を上底、もう片方の辺を下底と区別します。つまり、台形の面積を求める公式は、(上底+下底)×高さ÷2となります。上底+下底にカッコがついているのは、先に計算する必要があるからです。四則演算の優先順位は覚えておきましょう。
四則演算の順番
- 優先順位1:カッコの中
- 優先順位2:掛け算と割り算
- 優先順位3:足し算と引き算
三角形
三角形とは、同一直線状にない三点とそれらを結んでできる三つの線分からなる図形のことです。
三角形は長方形の半分とみなすことができます。また、台形の時と同じで、一辺の中点を回転軸として回転させて、元の三角形と合わせると平行四辺形になります。三角形の面積は長方形や平行四辺形の半分となります。つまり、三角形の面積を求める公式は、底辺×高さ÷2となります。底辺と高さを使いますので、平行四辺形の半分と考えた方が良いと思います。
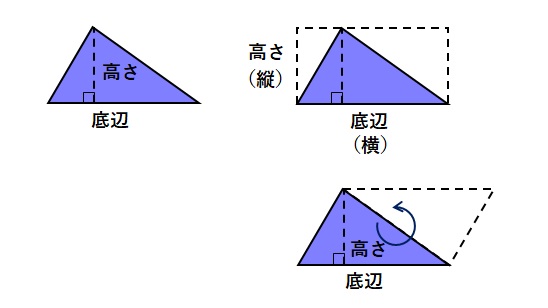
円
円とは、一定点から一定の距離にある点全体の作る図形のことです。
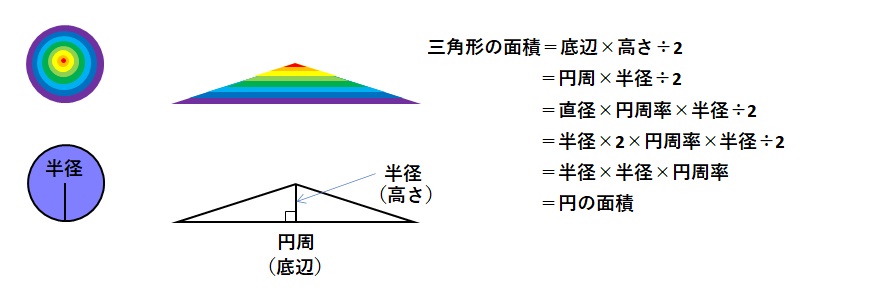
円の面積を求めるにあたり、円周率が円の直径に対する円周の長さの比率で、直径は半径の2倍であることを知っておく必要があります。円周を直線として積み上げれば、円の中心を頂点とした二等辺三角形が出来上がります。つまり、円の面積を求める公式は、半径×半径×円周率となります。
問題
次の三角形の面積を求めてください。公式を理解していたら簡単ですね。
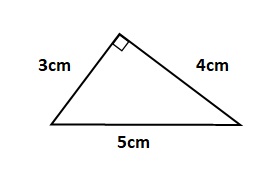
三角形の面積は底辺×高さで求まります。高さは垂直方向の長さのことでしたね。問題の三角形は3cmの辺と4cmの辺の間の角度が90度なので、底辺を3cmとしますと、高さは4cmとなります。従いまして、三角形の面積を求める式は3×4÷2となり、答えは6cm2となります。もちろん、底辺を4cm、高さを3cmとしても同じになります。
別解として、ヘロンの公式でも求められます。しかし、この問題に対しては先の方法よりも計算が面倒になるので、お勧めできません。
まとめ
公式をまとめると、次の図になります。
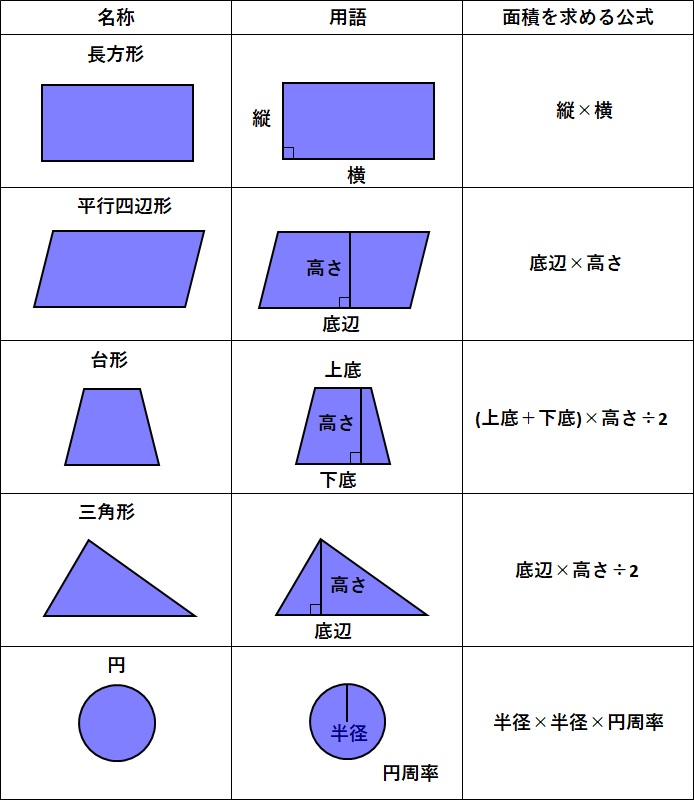
さて、面積についての説明はいかがでしたでしょうか。今回は、小学校で習う知識だけで面積を求める公式を導いてみました。本当なら、面積は積分を使って計算します。従いまして、長方形で説明した四辺の長さが1の正方形が何個敷き詰められるかというのは簡便的な説明になります。円の面積の説明も同様です。厳密な説明はできませんでしたが、本説明で理解していただき、数学の苦手意識を軽減することに貢献できたなら幸いです。


