2022年のセンター試験の数学が難しすぎるという記事を読んで、私が大学生のころ、中学2年生の生徒に「分数を分数で割る意味が分からない」と言われたことを思い出しました。当時は、正直、冗談だろうと思いました。私は数学が得意科目でしたので、分数同士の割り算の何が分からないのかが分からないという状況の中、説明を試みました。
さて、みなさんなら何と説明するでしょうか。小学生時代を思い出して、分数の割り算はひっくり返して掛けると説明するのでしょうか。
そもそも割り算は2つの場合に使用します。1つ目は単位当たりに分配するときで、2つ目は分配されたものを元に戻すときです。
少し分かりにくいと思いますので、距離と時間と速さの関係で考えてみましょう。速さとは単位時間あたりに進む距離のことを言い、単位時間を1時間とすれば速さは時速、1分間とすれば分速、1秒間とすれば秒速となります。速さの定義から考えますと、距離を時間で割ると速さが求まります。また、時間で分配されたので、元に戻すには距離を速さで割れば時間が求まります。
ここで問題です。
あなたは、800mの距離を10分かけて歩きました。さて、あなたは平均分速何mで歩いたことになるでしょうか?

途中式を省略せずに書くと、上のようになります。割られる数字は分子に、割る数字は分母にするのでしたね。そして、800と10は約分できますね。約分しないと答えのパターンが無限にできるのと、数学はシンプルにするのが美しいので、最小の数字となるように約分します。また、分母が1の場合は、記載しないのでしたね。(∵80÷1=80)
ここで、約分と倍分(次で使う)が何かを見てみましょう。

次に、
あなたは、800mの距離を10分かけて歩きました。さて、あなたは平均時速何kmで歩いたことになるでしょうか?
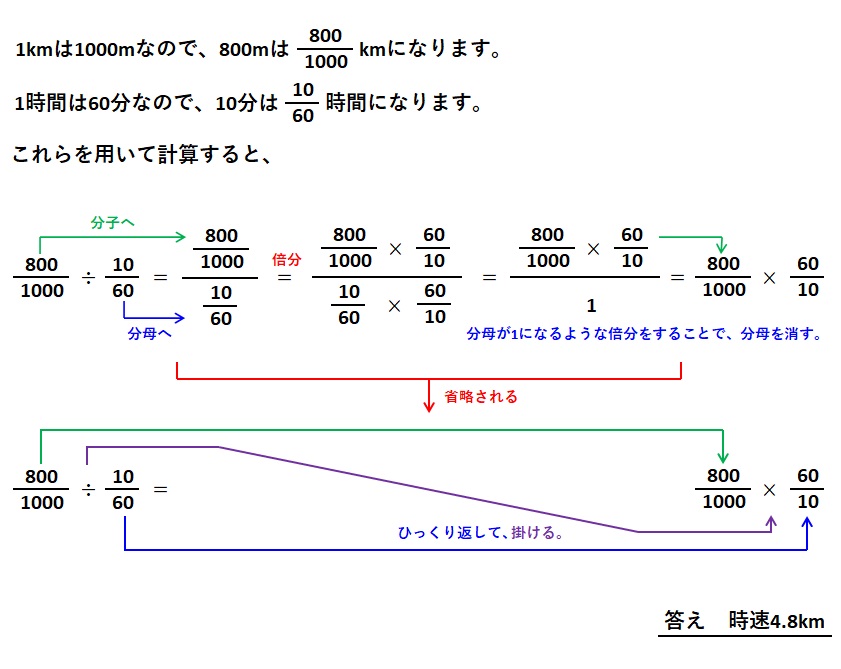
割られる数字と割る数字が両方とも分数ですが素直に、割られる分数を分子に、割る分数を分母にもっていきましょう。分母を1にすれば分母をなくせますので、分母が1になるように倍分します。最後の式を見てください。割る分数がひっくり返って掛け算になっていますね。つまり、倍分して分母を1にするために、ひっくり返して掛ける必要があるのです。
計算式での説明で分かっていただけましたでしょうか?「分数の割り算はひっくり返して掛ける、ひっくり返して掛ける、ひっくり返して掛ける・・・」呪文のように唱えて暗記することで意味が分からなくなるのではと想像します。また、途中式を省略することで、分かりにくさを助長しているのではないでしょうか。
次に、割り算が何をやっているのかを図で見てみましょう。
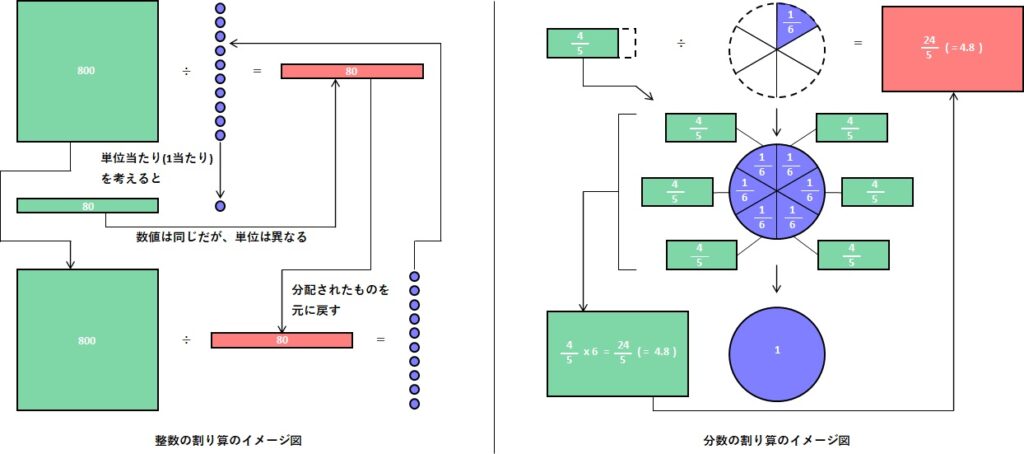
どうですか?イメージできたでしょうか。
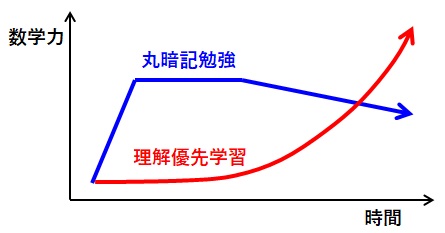
数学に関しては、公式を丸暗記して数値を当てはめるだけの勉強をしていては応用が利かなくなると思います。例えば、速さを求める考え方は圧力や密度などを求める問題にも活かせます。しかし、速さ、圧力や密度などを個別の公式としてとらえると、応用するのが難しくなります。公式を丸暗記して単に当てはめるだけの勉強をしていては、数学の能力は頭打ちになります。やがてその能力は、公式の数が増加するにつれ低下していくでしょう。
丸暗記:
速さを求めたい。→ 〇〇〇の公式に当てはめよう。→「き」÷「じ」→「は」が求まる。→ 計算して答えを書く。→ 採点する。→ 正解だ。→ 答えが合っていて良かった。→ 圧力を求めたい。→ 公式を探そう。→ 力÷面積で求まると書いている。→ 計算して答えを書く。→ ・・・
理解優先:
速さを求めたい。→ 速さとは単位時間あたりに進む距離だ。→ 距離÷時間で速さが求まるはずだ。→ 計算して答えを書く。→ 採点する。→ 正解だ。→ 考え方が合っていて良かった。→ 圧力を求めたい。→ 圧力とは単位面積あたりに垂直方向に押す力の大きさのことらしい。→ 速さと構造が似ているぞ。→ 垂直方向に押す力÷力がはたらく面積で求まりそうだ。→ 計算して答えを書く。→ ・・・
念のため記載しますが、私は暗記がいけないと言っているのではありません。なぜなら、用語の定義と数式の考え方は頭に入れておく必要があるからです。数学は積み重ねの科目なので、前に習った知識は理解していることを前提で新しいことを学びます。そのため、一つ一つ理解しておくことが重要となります。
さて、分数を分数で割る意味についての説明はいかがでしたでしょうか。本説明で理解していただき、数学の苦手意識を軽減することに貢献できたなら幸いです。


